Skip to main content

深度解析：ReLU 与 GELU 的全面对比

摘要： 本文档详细剖析了深度学习中两代核心激活函数——Rectified Linear Unit (ReLU) 与 Gaussian Error Linear Unit (GELU) 的异同。我们将从数学定义、概率解释、优化特性及误区澄清四个维度，解释为何 GELU 成为现代大模型（如 BERT, GPT, ViT）的首选。

1. 基础定义与直观对比​

1.1 ReLU (线性整流单元)​

定义： 深度学习早期的统治者，以其简单高效著称。

f(x)=max⁡(0,x)f(x) = \max(0, x)

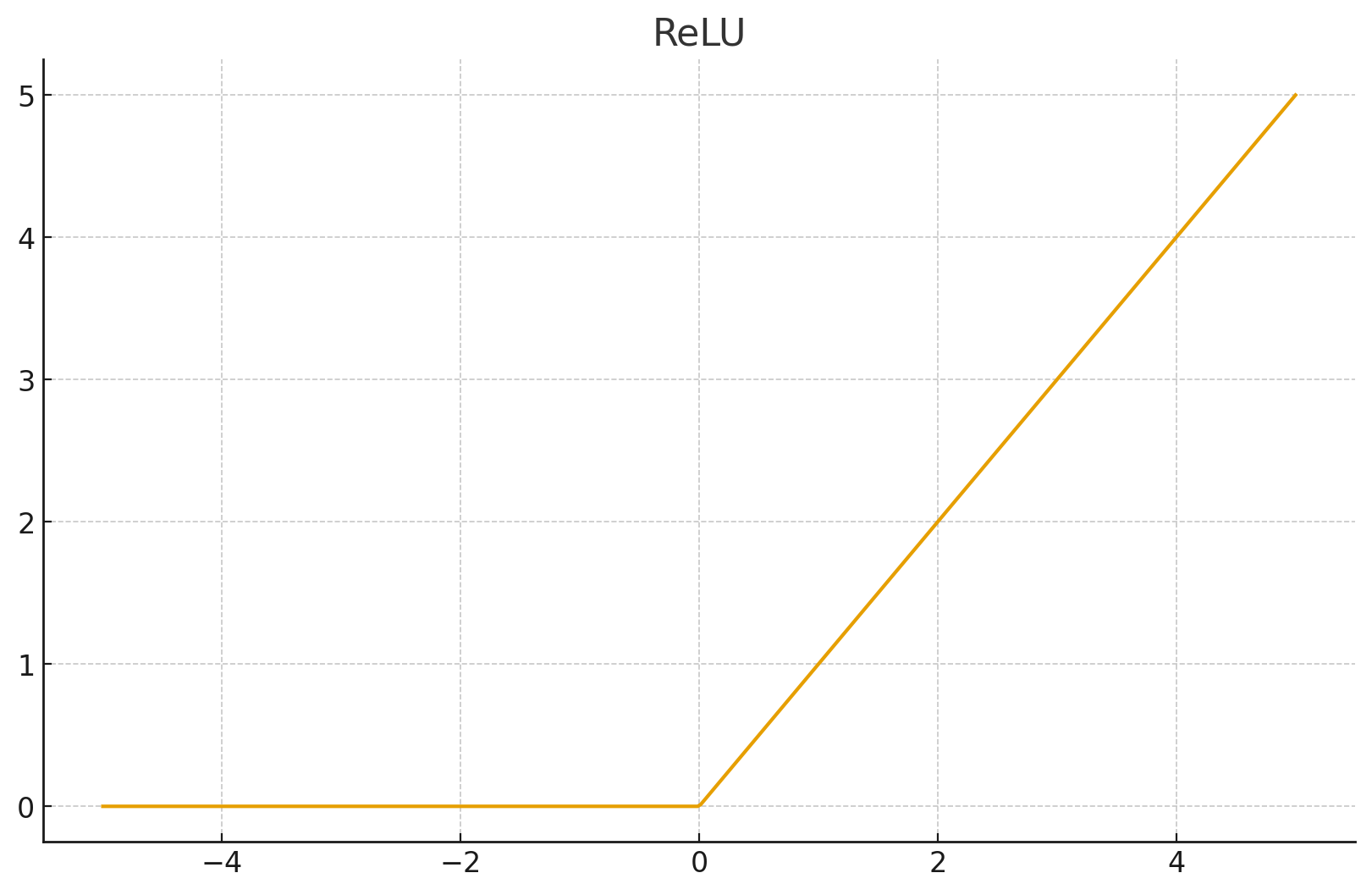
ReLU激活函数

逻辑： 是一个硬门控 (Hard Gate)。

行为：

  • 输入是正数？原样通过。
  • 输入是负数？直接封死（置0）。

几何特征： 由两条直线组成，在 x=0x=0 处有一个尖锐的"折角"。

1.2 GELU (高斯误差线性单元)​

定义： 结合了随机正则化（Dropout）思想的平滑激活函数。

f(x)=x⋅Φ(x)f(x) = x \cdot \Phi(x)

其中 Φ(x)\Phi(x) 是标准正态分布的累积分布函数 (CDF)。

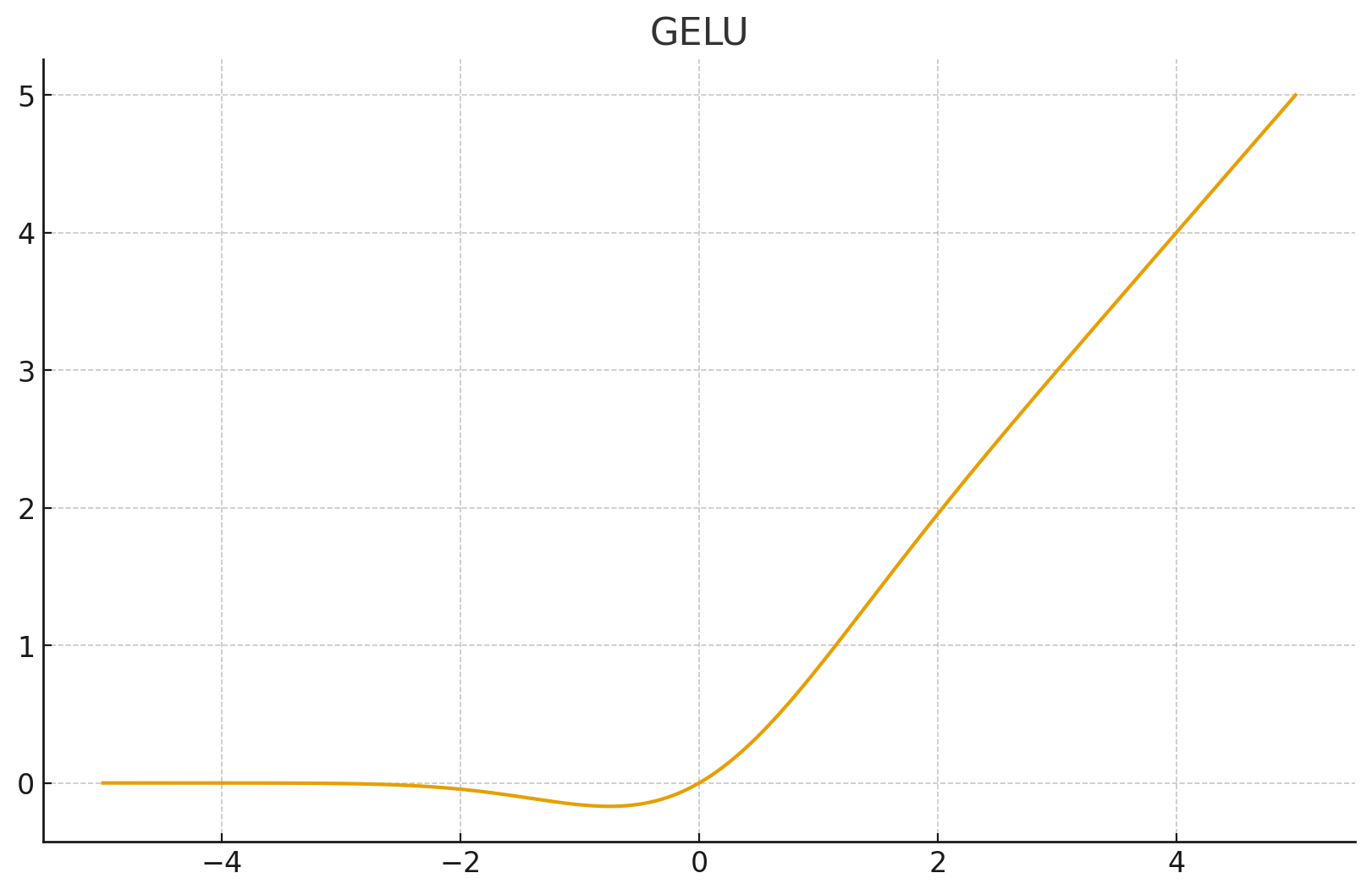
GELU激活函数

逻辑： 是一个软门控 (Soft Gate)。

行为：

  • 输入是正数？根据数值大小，按比例保留（数值越大保留越多，趋近于100%）。
  • 输入是负数？大概率抑制，但允许极少量信息通过（那个微小的负下凹）。

几何特征： 一条连续光滑的曲线，在 0 附近圆润过渡，且非单调（在负半轴有一个小坑）。

2. 核心差异深度剖析​

2.1 决定性 vs 概率性 (Deterministic vs Probabilistic)​

这是两者最本质的区别。

ReLU 是二值的： 它只看符号。0.00010.0001 和 100100 都被视为"通过"；−0.0001-0.0001 和 −100-100 都被视为"阻断"。它忽略了数值本身的统计意义。

GELU 是加权的： 它引入了概率的视角。

  • 它假设神经元的输入往往服从正态分布。
  • 它不仅仅问"你是正的吗？"，它问的是**"你在正态分布中排在什么位置？"**
  • xx 越小，它作为"噪音"的可能性越大，就被抑制得越厉害。

2.2 光滑性与梯度流 (Smoothness)​

ReLU 的问题： 在 x=0x=0 处不可导。虽然工程上我们人为定义导数为 0 或 1，但在深层网络的反向传播中，无数个"折角"叠加会造成优化曲面的不平整，影响收敛精度。

GELU 的优势： 二阶连续可导。无论 xx 在哪里，其梯度的变化都是平滑的。这意味着优化器（SGD/Adam）在"下山"时，地形是圆滑的坡道，而不是陡峭的台阶，这对于训练超深网络（如 100 层的 Transformer）至关重要。

2.3 非单调性 (The "Negative Dip")​

这是 GELU 最迷人的特性之一。

  • 看图时你会发现，GELU 在 x≈−1.0x \approx -1.0 到 00 之间，函数值其实是负数（虽然很小）。
  • ReLU 彻底抹杀了负半轴的信息，导致神经元"死亡"（Dead ReLU 问题）。
  • GELU 通过这个微小的负值区域，保留了梯度的回传能力。这赋予了神经元更复杂的表达能力——它不仅能表达"有"或"无"，还能表达某种程度的"反向抑制"。

3. 核心误区澄清：PDF vs CDF​

很多初学者容易混淆正态分布的概率密度函数 (PDF) 和 累积分布函数 (CDF)，导致误解 GELU 的权重机制。

概念形状含义GELU 用了吗？
PDF (钟形曲线)中间高，两头低"这个数值出现的概率是多少？"❌ NO! 如果用这个，大数值反而会被抑制。
CDF (S型曲线)从0爬升到1"这个数值打败了百分之多少的人？"✅ YES!

GELU 的加权逻辑：

Output=x×权重(CDF)\text{Output} = x \times \text{权重(CDF)}

  • 当 xx 很大 (如 +5)： CDF ≈1\approx 1。意思是"你打败了99.9%的噪音，你是有效信号"。结果 ≈x×1=x\approx x \times 1 = x (回归 ReLU)。
  • 当 xx 很小 (如 -5)： CDF ≈0\approx 0。意思是"你比99.9%的信号都弱，你大概率是噪音"。结果 ≈x×0=0\approx x \times 0 = 0。
  • 当 xx 接近 0： CDF ≈0.5\approx 0.5。意思是"半信半疑，折个中"。

4. 总结：该怎么选？​

特性ReLUGELU
计算速度⚡ 极快 (仅需比较大小)🐢 较慢 (涉及 tanh 或 erf 运算)
适用领域🖼️ 计算机视觉 (CNN, ResNet)📝 自然语言处理 (Transformer, BERT, GPT)
收敛性⚠️ 容易出现 Dead ReLU✅ 更稳健，允许微负梯度
精度👍 足够好 (Good Enough)🏆 往往能提升 SOTA 精度 (State of the Art)

一句话建议：​

如果是做 CNN 图像分类，ReLU 依然是性价比之王；但如果是做 Transformer、大模型或复杂的生成任务，请无脑选择 GELU。