Skip to main content

激活函数

第一代：经典饱和型 (Saturated)​

特点： 有上下界，容易导致梯度消失（Gradient Vanishing），目前在隐藏层中已较少使用。

1. Sigmoid​

应用场景： 二分类问题的输出层、LSTM/GRU 的门控单元。

  • 数学公式： σ(x)=11+e−x\sigma(x) = \frac{1}{1 + e^{-x}}
  • 取值范围： (0,1)(0, 1)
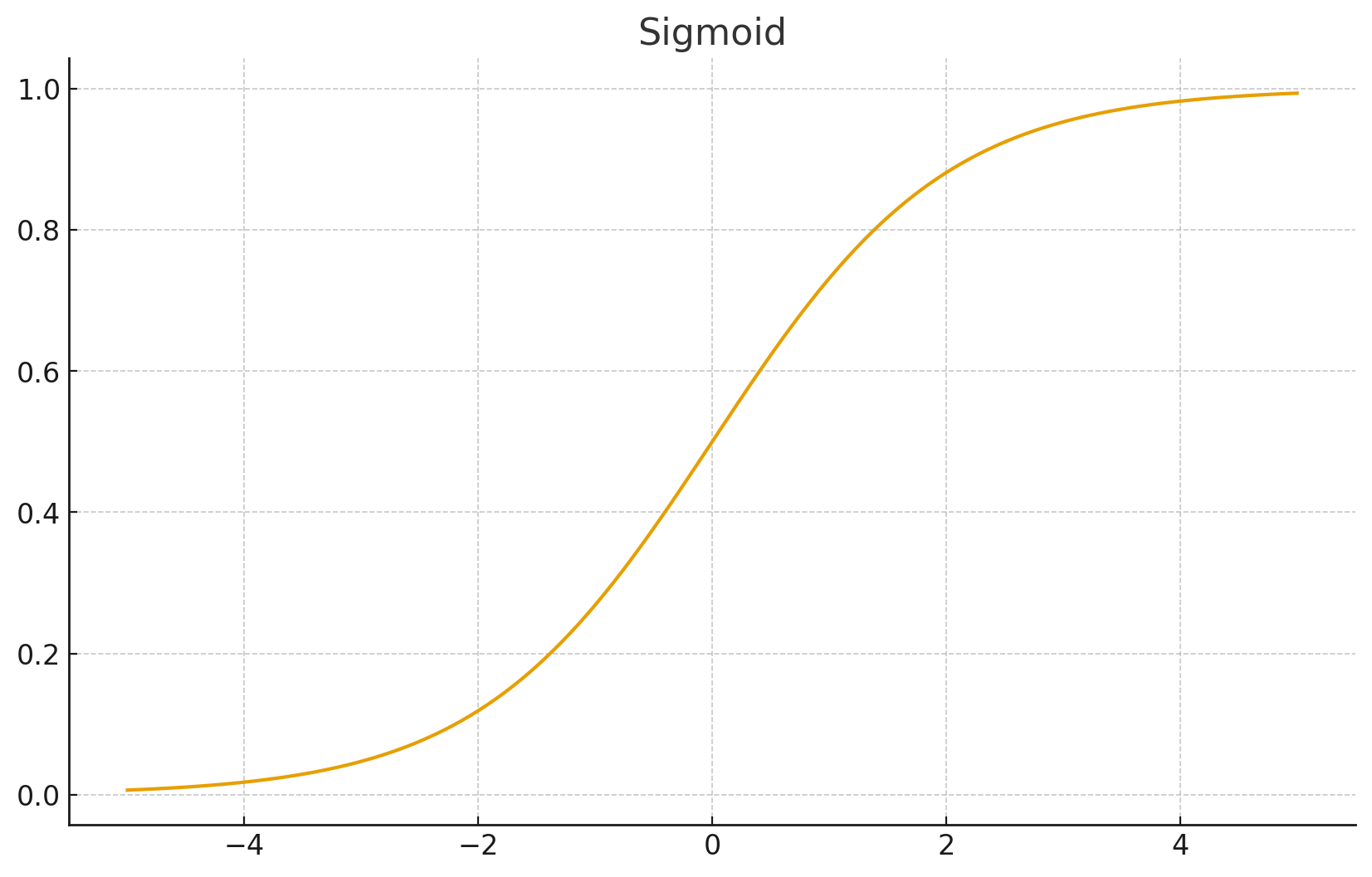
Sigmoid激活函数
  • 优点： 输出模拟概率，物理意义清晰。
  • 缺点：
    1. 梯度消失： 当 xx 很大或很小时，梯度趋近于 0，导致反向传播无法更新权重。
    2. 不以 0 为中心 (Not Zero-Centered)： 导致收敛变慢。
    3. 计算昂贵： 包含指数运算。
  • PyTorch 实现： 
    import torch.nn as nn
    act = nn.Sigmoid()
    # 或 F.sigmoid(x) (不推荐，建议用 torch.sigmoid)

2. Tanh (双曲正切)​

应用场景： RNN/LSTM 的状态更新，生成对抗网络 (GAN) 的最后一层（将数据映射到 -1 到 1）。

  • 数学公式： tanh⁡(x)=ex−e−xex+e−x\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}
  • 取值范围： (−1,1)(-1, 1)
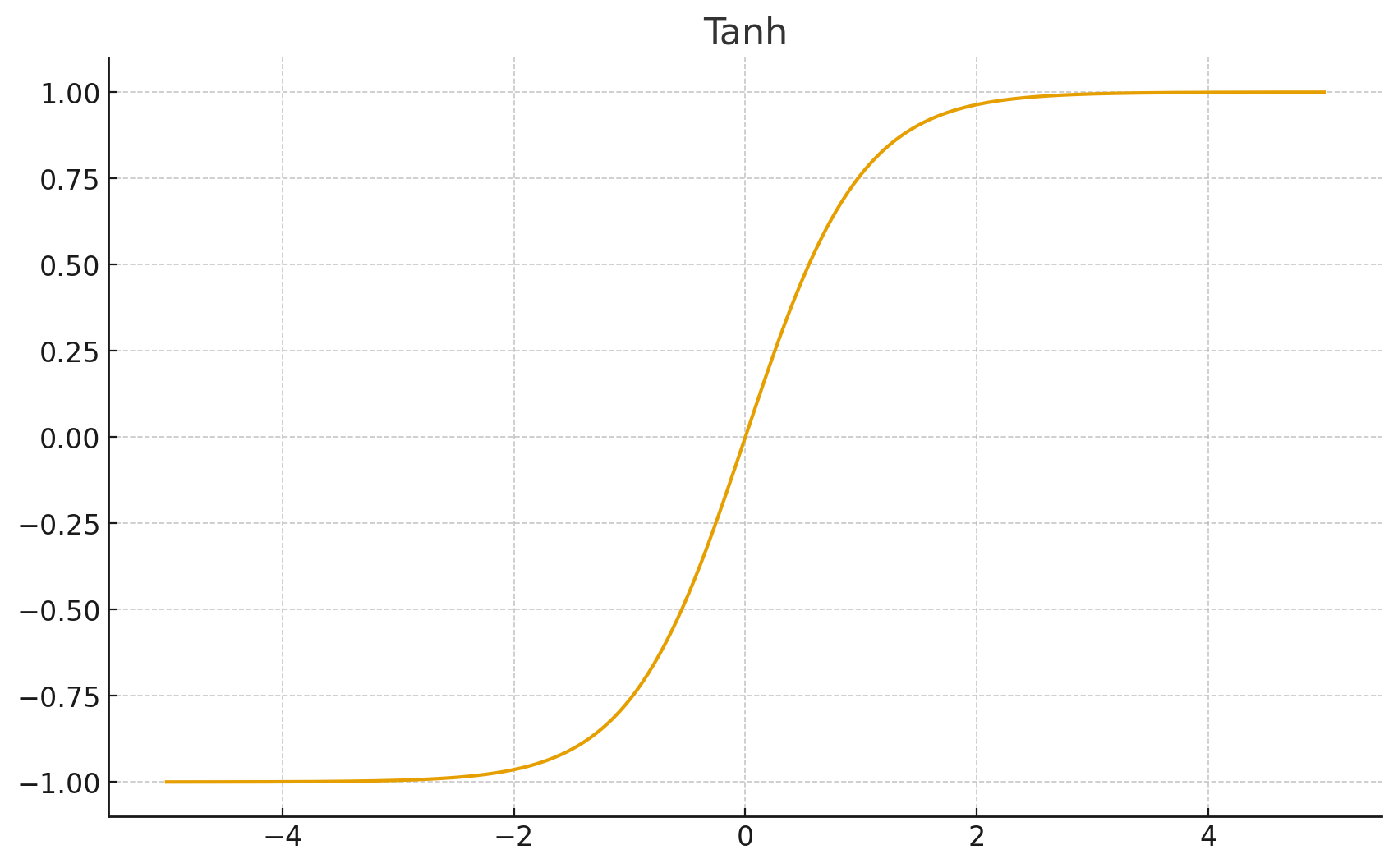
Tanh激活函数
  • 优点： 解决了 Sigmoid 不以 0 为中心的问题，收敛通常比 Sigmoid 快。
  • 缺点： 依然存在严重的梯度消失问题。
  • PyTorch 实现： 
    act = nn.Tanh()

第二代：分段线性型 (Rectified)​

特点： 也就是 ReLU 家族，解决了梯度消失问题，是 CNN 的标配。

3. ReLU (Rectified Linear Unit)​

应用场景： 绝大多数卷积神经网络 (CNN) 和全连接层的首选默认激活函数。

  • 数学公式： f(x)=max⁡(0,x)f(x) = \max(0, x)
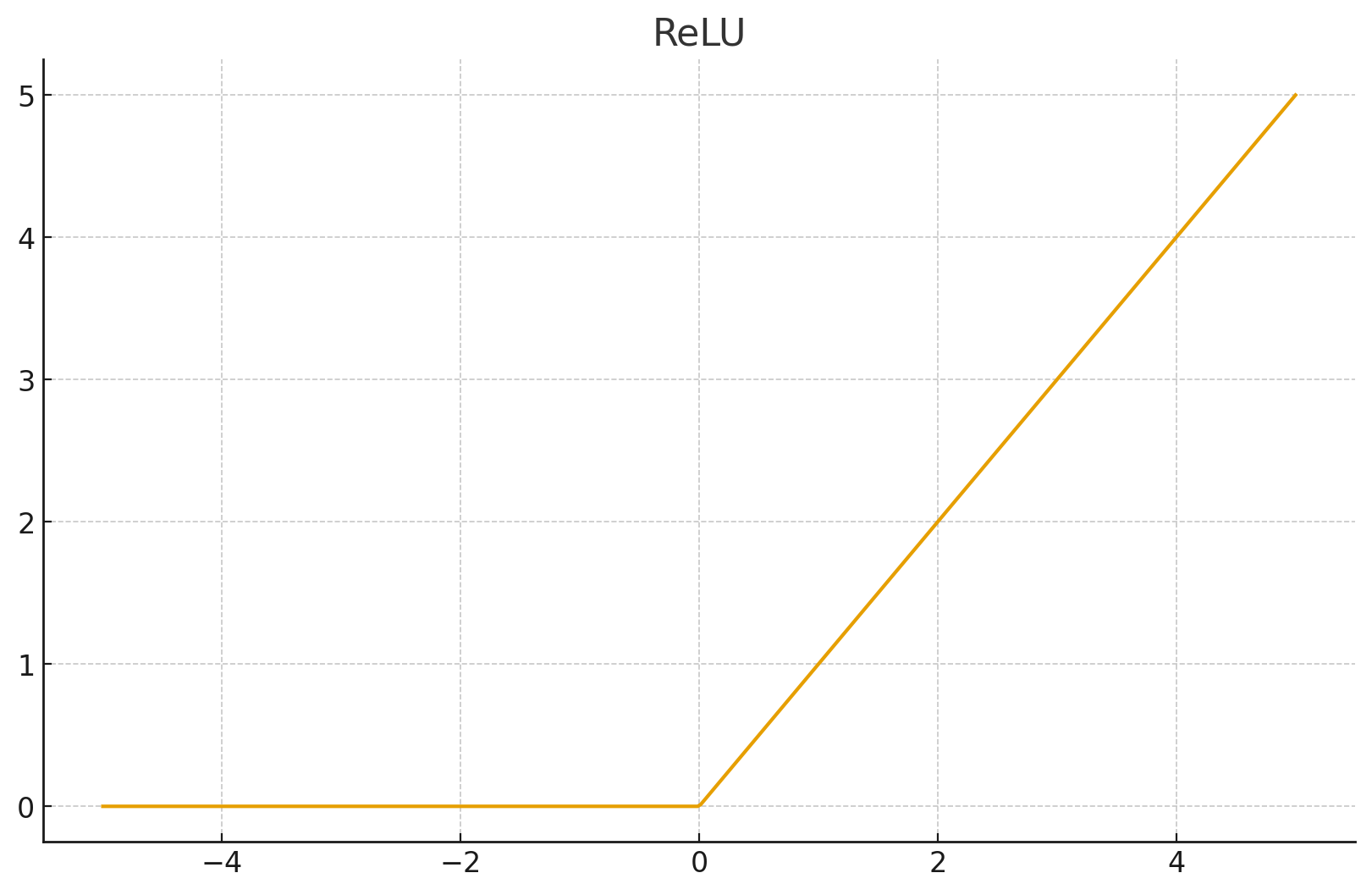
ReLU激活函数
  • 特点：
    • 正区间梯度为 1： 彻底解决正区间的梯度消失问题。
    • 计算极快： 只需要判断是否大于 0。
    • 稀疏性： 让一部分神经元输出 0，模拟生物神经元的稀疏激活。
  • 缺点 (Dead ReLU)： 如果输入是负数，梯度为 0，神经元彻底“死亡”，不再更新。
  • PyTorch 实现： 
    # inplace=True 可以节省显存，直接在原变量上修改
    act = nn.ReLU(inplace=True)

4. Leaky ReLU​

应用场景： 解决 Dead ReLU 问题，常用于 GAN 的判别器 (Discriminator)。

  • 数学公式： f(x)=max⁡(αx,x)f(x) = \max(\alpha x, x) 其中 α\alpha 通常是一个很小的常数（如 0.01）。
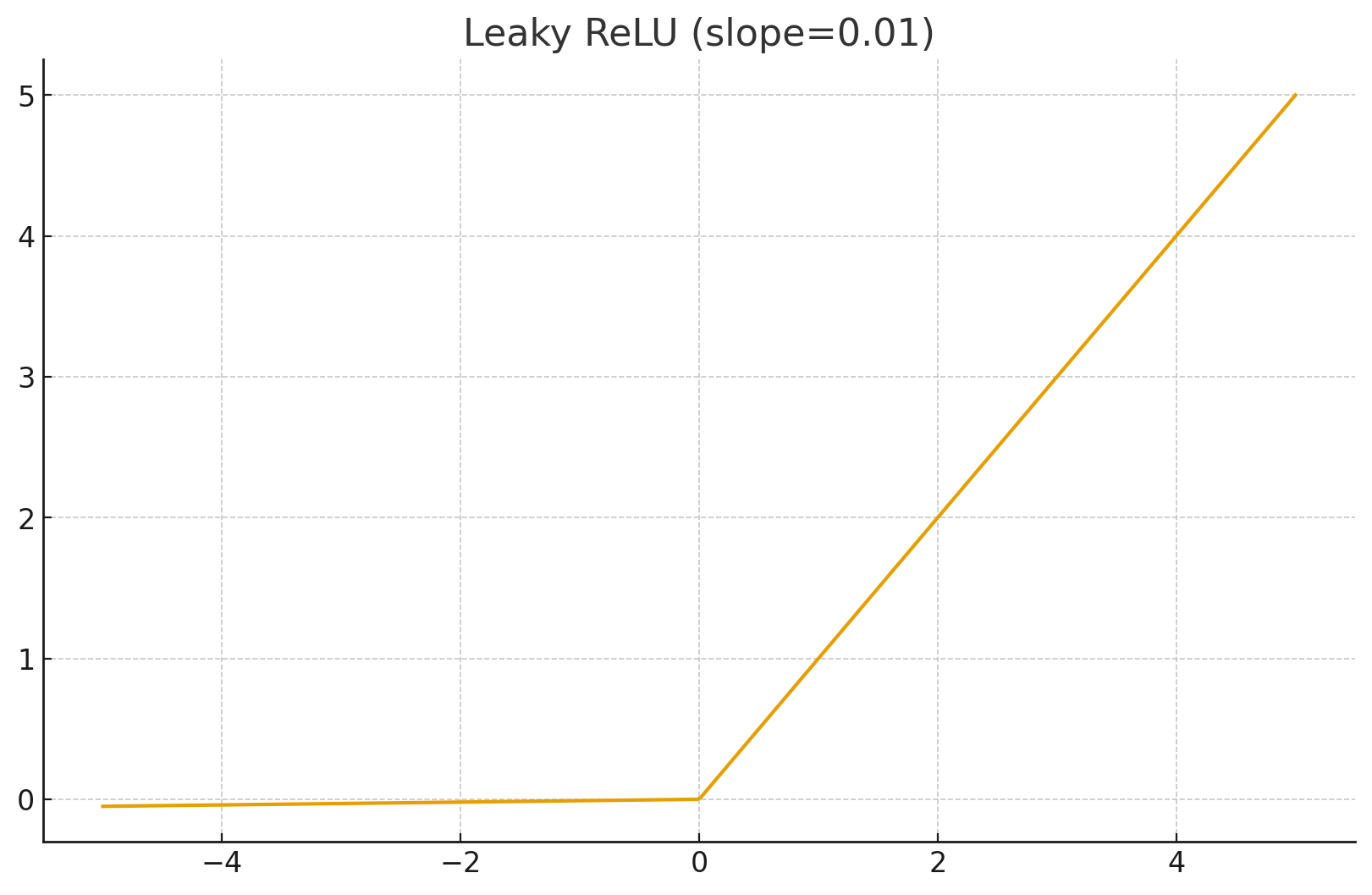
Leaky ReLU激活函数
  • 特点： 负区间给一个很小的斜率，保证梯度不为 0。
  • PyTorch 实现： 
    act = nn.LeakyReLU(negative_slope=0.01, inplace=True)

5. PReLU (Parametric ReLU)​

  • 特点： 将 Leaky ReLU 中的斜率 α\alpha 变成一个可学习的参数，让网络自己决定负半轴怎么激活。
  • PyTorch 实现： 
    # num_parameters=1 表示所有通道共用一个 alpha
    # num_parameters=channels 表示每个通道由独立的 alpha
    act = nn.PReLU(num_parameters=1)

第三代：现代平滑型 (Smooth & Gated)​

特点： 非单调、平滑，在 Transformer (BERT/GPT) 和现代 CNN (EfficientNet/YOLOv5+) 中表现优异。

6. GELU (Gaussian Error Linear Unit)​

应用场景： BERT, GPT-3, ViT (Vision Transformer) 的标配。

  • 原理： 可以看作是"平滑版的 ReLU"。它不是直接截断负值，而是根据正态分布的累积分布函数 Φ(x)\Phi(x) 对输入进行加权。
  • 数学公式（近似）： GELU(x)≈0.5x(1+tanh⁡(2/π(x+0.044715x3)))GELU(x) \approx 0.5x(1 + \tanh(\sqrt{2/\pi}(x + 0.044715x^3))) 或者简单理解为：x⋅P(X≤x)x \cdot P(X \le x)。
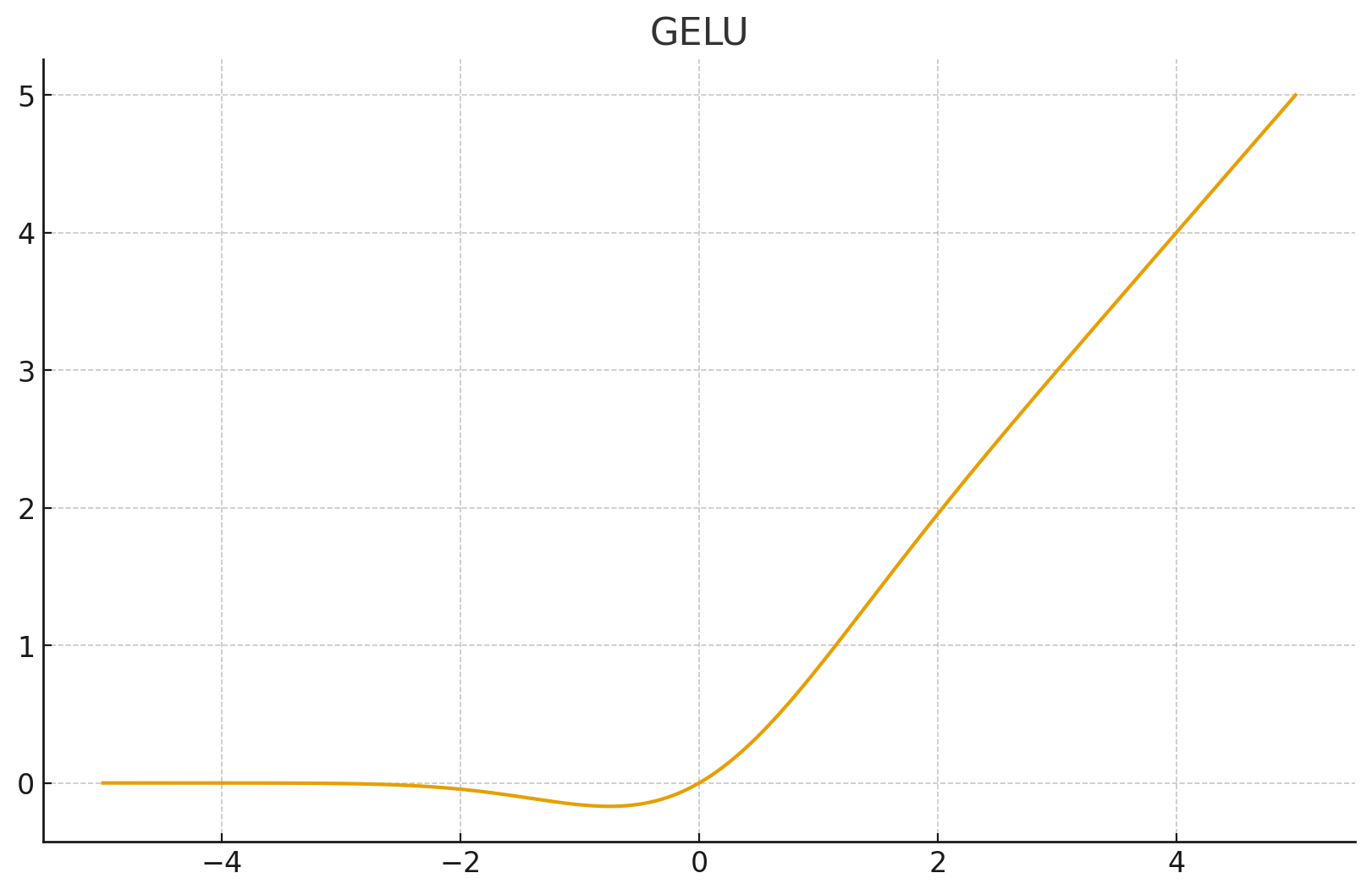
GELU激活函数
  • 优点： 在 0 附近是平滑弯曲的，且允许微小的负值输出。实验证明在深层 Transformer 中比 ReLU 效果好。
  • PyTorch 实现： 
    act = nn.GELU()

7. SiLU (Sigmoid Linear Unit) / Swish​

应用场景： YOLOv5, YOLOv8, EfficientNet 的标配。

  • 数学公式： SiLU(x)=x⋅σ(x)=x1+e−x\text{SiLU}(x) = x \cdot \sigma(x) = \frac{x}{1 + e^{-x}}
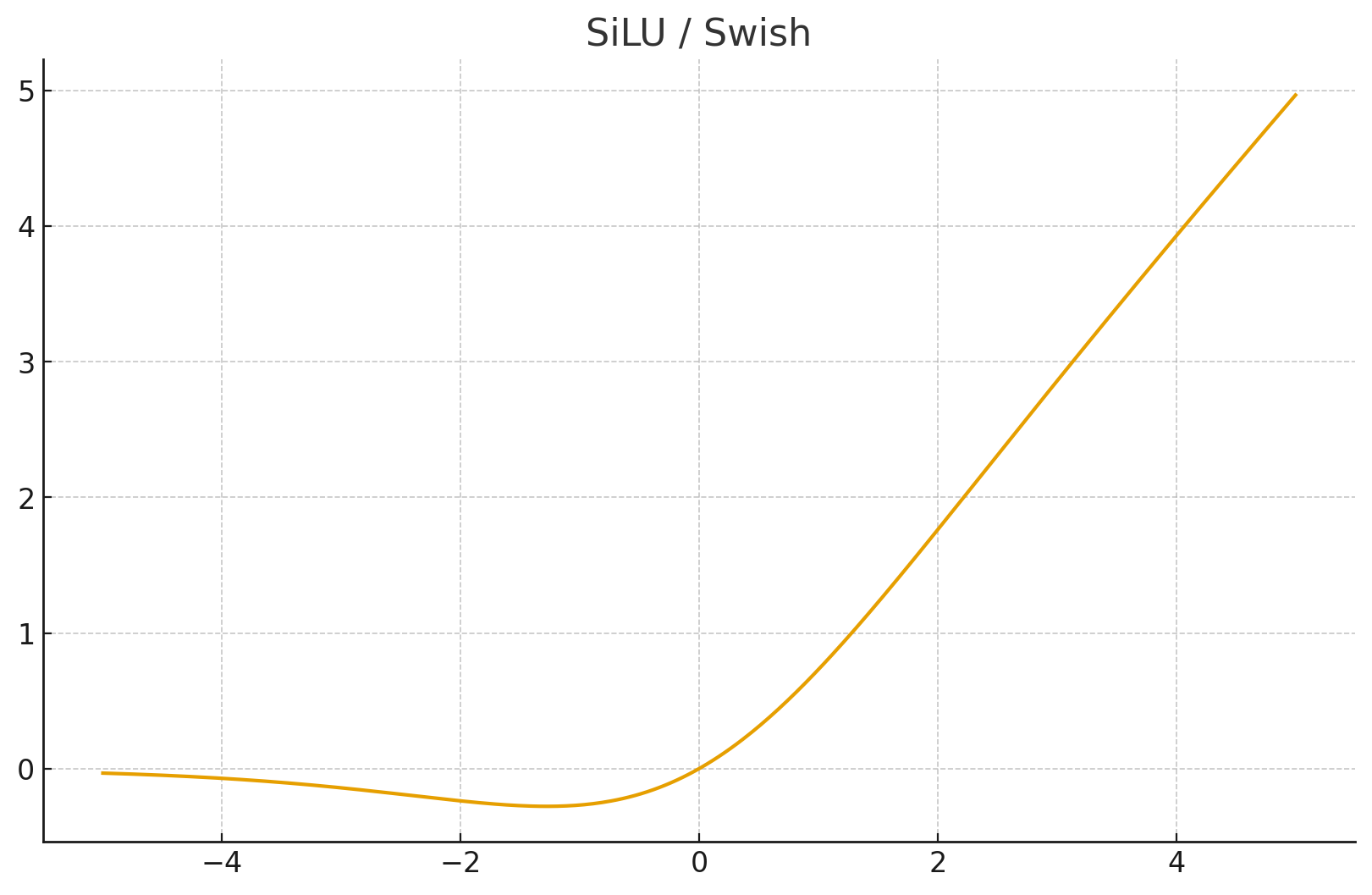
SiLU/Swish激活函数
  • 特点： 它是 x 乘以自己的 Sigmoid。
    • 自门控 (Self-gated)： 输入值决定了通过的比例。
    • 非单调： 在负半轴有一个很小的“波谷”，不仅非线性，还非单调，这被证明对深层网络优化很有帮助。
  • PyTorch 实现： 
    # PyTorch 1.7+ 内置
    act = nn.SiLU() 
    # 老版本可能叫 nn.SiLU 或需要自己写 (x * torch.sigmoid(x))

特殊用途：输出层专用​

8. Softmax​

应用场景： 多分类问题的输出层。

  • 数学公式： Softmax(xi)=exi∑jexj\text{Softmax}(x_i) = \frac{e^{x_i}}{\sum_{j} e^{x_j}}
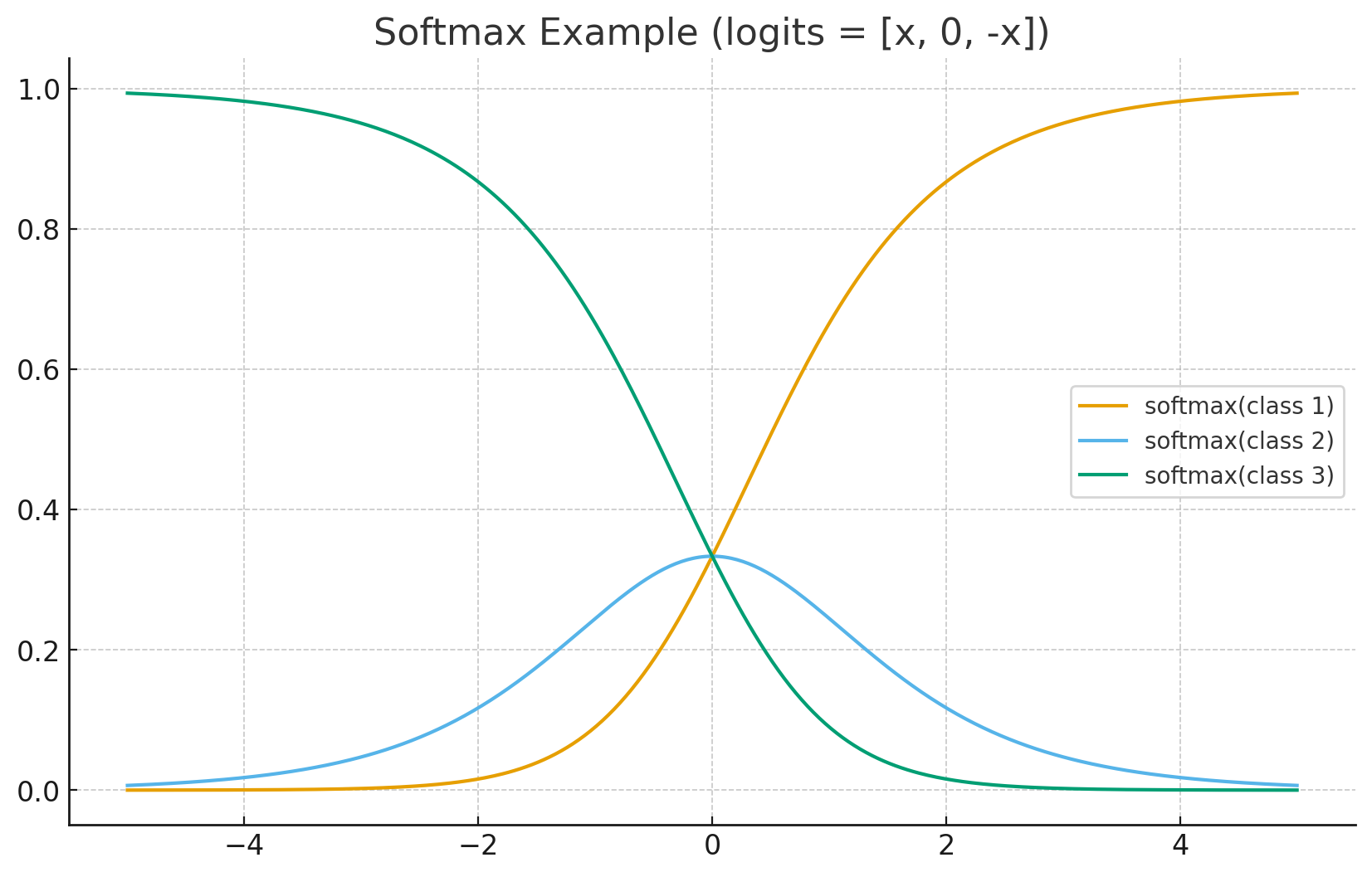
Softmax激活函数
  • 作用：
    1. 将数值映射到 (0,1)(0, 1)。
    2. 所有输出之和为 1（概率分布）。
    3. 放大差异： 指数函数会把大的值放得更大，小的值压得更小（强者恒强）。
  • PyTorch 实现： 
    # dim=1 表示在类别维度上进行 Softmax
    act = nn.Softmax(dim=1)

总结与选型指南 (Cheat Sheet)​

激活函数核心特点最佳适用场景避坑指南
Sigmoid输出(0,1)，容易梯度消失二分类输出层不要在深层网络的隐藏层使用。
Tanh输出(-1,1)，零中心RNN/LSTM 隐藏层依然有梯度消失风险，CNN/Transfomer 慎用。
ReLU简单、粗暴、有效CNN/MLP 默认首选如果学习率过大，可能会出现 Dead ReLU。
Leaky ReLU负区有梯度GAN 的判别器，或 ReLU 效果不好时通常 α=0.01\alpha=0.01 即可。
GELU平滑、概率性质Transformer (GPT/BERT)计算量比 ReLU 略大，但效果更好。
SiLU (Swish)自门控、非单调Modern CNN (YOLO/EfficientNet)现代视觉模型的首选。

简单的一句话建议：

  • 做 NLP (Transformer)：闭眼选 GELU。
  • 做 视觉 (CNN/YOLO)：首选 ReLU，追求更高精度换 SiLU。
  • 做 简单的全连接网络：ReLU 最稳。
  • 输出层：二分类用 Sigmoid，多分类用 Softmax。